Короткопериодные стоячие волны создаются в результате сложения (интерференции) поступательных волн, распространяющихся в противоположных направлениях.
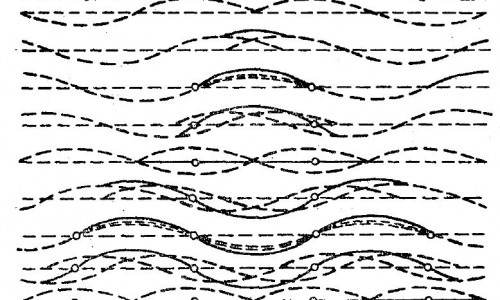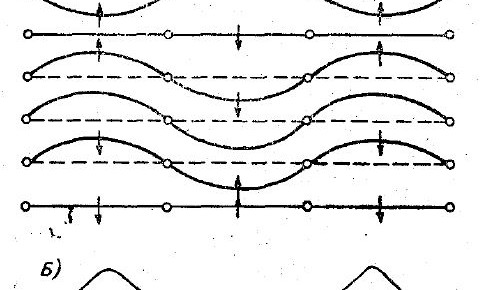
Образование таких волн наглядно показано на примере сложения двух одинаковых (по высоте, длине и периоду) волн от момента их встречи и далее через каждые 1/8, 2/8...8/8 в периода (рис. 1); для упрощения построения взяты синусоидальные волны. Колебания водной поверхности (через 1/8 периода), когда на ней уже образовались стоячие волны, представлены на рис. 2.А.
Из рассмотрения этих рисунков следует, что в стоячих волнах амплитуда у всех частиц разная и все частицы, расположенные между двумя соседними узлами, т. е. точками, в которых вертикальные колебания отсутствуют (на рисунках показаны точками, обведенными кружками), одновременно начинают подниматься вверх или опускаться вниз, т. е. находятся в одной и той же фазе. Частицы, находящиеся на одинаковых расстояниях по обе стороны узла, колеблются одинаково, но направления колебаний их прямо противоположны. При переходе через узел фаза сразу меняется на противоположную.
В пучности, т. е. посредине между двумя соседними узлами, амплитуда колебания частиц вдвое больше амплитуды каждой из двух одинаковых интерферирующих волн из которой образовалась стоячая волна, или промежутку времени между двумя последующими пучностями.
Длина стоячей волны равна длине поступательной волны, из которой она образовалась, или удвоенному расстоянию между соседними узлами.
Рис. 1 Схема образования стоячих волн из двух одинаковых синусоидальных волн
Элементы результирующей волны остаются постоянными только в том случае, если элементы складывающихся волн совершенно одинаковы и волны различаются только по фазе. В противном случае высота и длина, результирующей волны являются переменными и наблюдается явление, называемое биением. Весьма неправильное биение создается также при сложении двух совершенно одинаковых волн, но не синусоидальной, а трохоидальной формы, у которых гребневая часть несимметрична подошвенной.
На рис. 2.Б представлено девять последовательных профилей волн, образующихся в результате сложения двух распространяющихся в противоположных направлениях трохоидальных волн одной и той же высоты и длины и с отношением высоты к длине, равным 1:4.
Форма стоячей волны за ее период, как видно на этом рисунке, непрерывно меняется, достигая удвоенной величины амплитуды слагаемых волн в пучностях и уменьшаясь в узлах, но не доходит до нуля.
В природе явление стоячих волн наблюдается сравнительно редко, например при отражении поступательных волн от приглубого берега (при углах наклона 45° и выше), когда элементы отраженных от берега волн те же, что и подходящих к берегу поступательных волн. Значительно чаще это явление наблюдается перед инженерными сооружениями, имеющими вертикальную лицевую стену или крутые откосы (>45°).
Рис. 2 Схема стоячих волн, образовавшихся из одинаковых синусоидальных (А) и трохоидальных (Б) волн (по Н. Н. Зубову)
Правильные двухмерные стоячие волны образуются при этом в том случае, если аналогичные поступательные волны распространяются по нормали к берегу. Если же волны подходят к берегу под острым углом, то под тем же углом они и отражаются, и в результате создаются правильные трехмерные стоячие волны.
При сложении волн (большей частью неодинаковых по элементам), приходящих с разных направлений, что особенно часто встречается на озерах, расположенных на дне глубоких горных котловин, где направление ветра тесно связано с местными особенностями рельефа, образуется толчея.
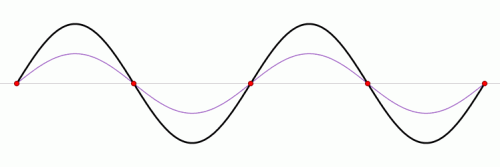
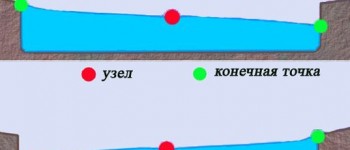
Пример стоячей волны
Пример стоячей волны (чёрная линия), возникшей в результате интерференции двух гармонических волн (красная и синяя линии) одинаковой частоты и амплитуды, распространяющихся во встречных направлениях.
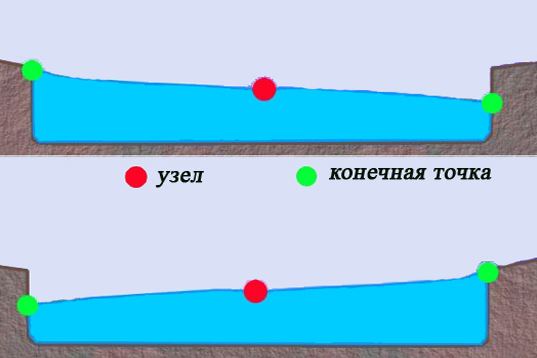
Красные точки обозначают узлы - точки или области в пространстве, в которых амплитуда колебательного процесса минимальна и равна разности амплитуд интерферирующих волн (амплитуда стоячей волны в узлах равна нулю).
Посередине между каждой парой соседних узлов располагается пучность - точка или область в пространстве, в которой амплитуда максимальна и равна сумме амплитуд интерферирующих волн (амплитуда стоячей волны в пучностях вдвое больше амплитуды каждой из интерферирующих волн).
Фаза колебательного процесса стоячей волны при переходе через узел меняется на 180° (говорят, что колебания синфазны в пространстве с точностью до 180°). В данном примере расстояние между соседними узлами составляет половину длины волны интерферирующих волн, значение коэффициента стоячей волны (отноношение амплитуд колебаний в пучности и узле) стремится к бесконечности.
